A análise combinatória estuda dois tipos de agrupamentos: Arranjos e combinações. Sendo que diferem em arranjos simples, combinações simples.
Arranjos são agrupamentos nos quais a ordem dos seus elementos faz a diferença. Por exemplo, os números de três algarismos formados pelos elementos {1, 2 e 3} são:
312, 321, 132, 123, 213, 231
Esse agrupamento é um arranjo, pois a ordem dos elementos 1, 2 e 3 diferem. E é considerado simples, pois os elementos não se repetem.
Para que tenhamos arranjos simples é preciso ter um conjunto de elementos distintos com uma quantidade qualquer de elementos, sendo que os arranjos simples formados irão possuir n elementos, sendo que essa quantidade será igual ou menor que a quantidade de elementos do conjunto.
Fórmula do Arranjo Simples
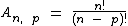
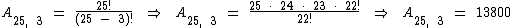
Veja o exemplo abaixo:
Dado o conjunto B = {5,6,7}, veja os possíveis agrupamentos formados com 2 elementos de B.

Então, os agrupamentos formados com 2 elementos do conjunto b são: 56,57,65,67,75,76. Esse agrupamento é formado por arranjos simples pelos elementos do conjunto B.
Nesse exemplo percebemos que é possível formar 6 arranjos, essa quantidade pode ser representada da seguinte forma: A3,2 (três elementos distintos formados de dois a dois). Utilizando o processo do princípio fundamental da contagem, calculamos a quantidade de elementos:
A3,2 = 3 . 2 . 1 = 6
Se em um agrupamento compararmos os arranjos simples formados perceberemos que eles se diferem de duas maneiras diferentes: pela ordem de seus elementos ou pela natureza de seus elementos. Por exemplo:
Se compararmos os arranjos 56 e 65 do exemplo anterior, perceberemos que eles são diferentes pela ordem dos seus elementos.
Se compararmos os arranjos 75 e 76 do exemplo anterior, perceberemos que eles são diferentes pela natureza de seus elementos, pois são diferentes.
Considerando n a quantidade de elementos de um conjunto qualquer e p um número natural menor ou igual a n. p será a classe ou a ordem do arranjo. Indicado da seguinte forma: A n , p
A fórmula geral utilizada no cálculo da quantidade de arranjos simples é:
.jpg)
Exemplo 2:
Quantas “palavras” (com sentido ou não) de 5 letras distintas podemos formar com as 20 primeiras letras do nosso alfabeto?
Não é necessário montar todas os arranjos possíveis para saber a sua quantidade, basta aplicar a fórmula:
Arranjos são agrupamentos nos quais a ordem dos seus elementos faz a diferença. Por exemplo, os números de três algarismos formados pelos elementos {1, 2 e 3} são:
312, 321, 132, 123, 213, 231
Esse agrupamento é um arranjo, pois a ordem dos elementos 1, 2 e 3 diferem. E é considerado simples, pois os elementos não se repetem.
Para que tenhamos arranjos simples é preciso ter um conjunto de elementos distintos com uma quantidade qualquer de elementos, sendo que os arranjos simples formados irão possuir n elementos, sendo que essa quantidade será igual ou menor que a quantidade de elementos do conjunto.
Fórmula do Arranjo Simples
Ao trabalharmos com arranjos simples, com n elementos distintos, agrupados p a p, com p ≤ n, podemos recorrer à seguinte fórmula:
Neste mesmo exemplo, utilizando a fórmula temos:
Veja o exemplo abaixo:
Dado o conjunto B = {5,6,7}, veja os possíveis agrupamentos formados com 2 elementos de B.
Então, os agrupamentos formados com 2 elementos do conjunto b são: 56,57,65,67,75,76. Esse agrupamento é formado por arranjos simples pelos elementos do conjunto B.
Nesse exemplo percebemos que é possível formar 6 arranjos, essa quantidade pode ser representada da seguinte forma: A3,2 (três elementos distintos formados de dois a dois). Utilizando o processo do princípio fundamental da contagem, calculamos a quantidade de elementos:
A3,2 = 3 . 2 . 1 = 6
Se em um agrupamento compararmos os arranjos simples formados perceberemos que eles se diferem de duas maneiras diferentes: pela ordem de seus elementos ou pela natureza de seus elementos. Por exemplo:
Se compararmos os arranjos 56 e 65 do exemplo anterior, perceberemos que eles são diferentes pela ordem dos seus elementos.
Se compararmos os arranjos 75 e 76 do exemplo anterior, perceberemos que eles são diferentes pela natureza de seus elementos, pois são diferentes.
Considerando n a quantidade de elementos de um conjunto qualquer e p um número natural menor ou igual a n. p será a classe ou a ordem do arranjo. Indicado da seguinte forma: A n , p
A fórmula geral utilizada no cálculo da quantidade de arranjos simples é:
.jpg)
Exemplo 2:
Quantas “palavras” (com sentido ou não) de 5 letras distintas podemos formar com as 20 primeiras letras do nosso alfabeto?
Não é necessário montar todas os arranjos possíveis para saber a sua quantidade, basta aplicar a fórmula:
A n , p = n!
(n – p)!
Sendo que o conjunto é formado por 20 elementos (n = 20) que serão unidos de 5 em 5 (p = 5). Substitua a fórmula.
.jpg)
(n – p)!
Sendo que o conjunto é formado por 20 elementos (n = 20) que serão unidos de 5 em 5 (p = 5). Substitua a fórmula.
.jpg)
Portanto, a quantidade de arranjos formados com as 20 primeiras letras do nosso alfabeto unidas de 5 em 5 é 1860480.

Nenhum comentário:
Postar um comentário